MLCA Week 10:

class: center, middle, inverse, title-slide

# MLCA Week 10:
## k-Nearest Neighbors
### Mike Mahoney
### 2021-11-03

---

.bg-washed-green.b--dark-green.ba.bw2.br3.shadow-5.ph4.mt5[

The introduction of numbers as coordinates is an act of violence.

.tr[
— Hermann Weyl: Philosophy of Mathematics and Natural Science
]
]

---
class: middle center

# k-Nearest Neighbors

# and Kernel-Based ML

---

Today we're going to switch gears and stop talking about tree-based models.

Our last two methods are examples of what are known as **kernel-based models**
(or **kernel machines**).

However, I don't necessarily want to spend a ton of
time today getting into the math behind what a "kernel" is.

Instead, for this class we can think about these models as being 
**distance-based methods**, which make predictions based on how _close_ an
observation is to other data in the training set.

---

The method we'll walk through first is called **k-nearest neighbors** (KNN), 
which bases its predictions based on some number ("k") of the closest points to 
your unknown observation.

KNN is almost never the best model for the job. First proposed in 1951, KNN
is incredibly computationally inefficient, is very slow to predict on most data,
and rarely if ever is as accurate as a well-tuned random forest or
GBM.

However, KNN models are simple to understand and use, are somewhat common in the 
literature given their age, and will help to set up our final model next week. 
As a result, it makes sense for us to walk through them here.

---

Let's say that you've just gotten back from the field, where you measured the 
size and greenness of a bunch of plants in both interior and edge forests.

You plot your data and it looks like this:

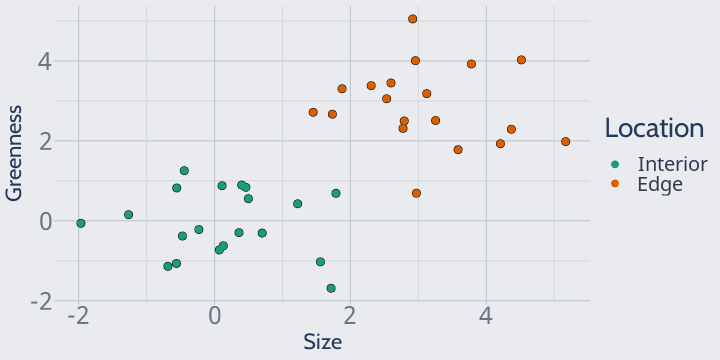
![](week_10_slides_files/figure-html/unnamed-chunk-1-1.png)

---

Unfortunately, though, you forgot to label where one of your plants was sampled
from.

When you add this plant to the plot, it looks like this:

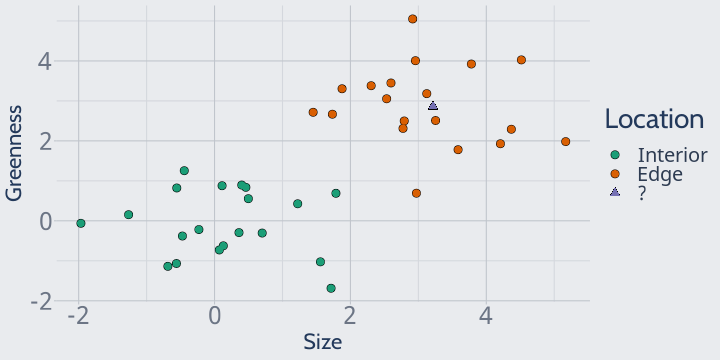
![](week_10_slides_files/figure-html/unnamed-chunk-2-1.png)

Can you guess where the plant was found?

---

We can easily assume the plant was found on a forest edge, because it's right in
the middle of the rest of our edge observations.

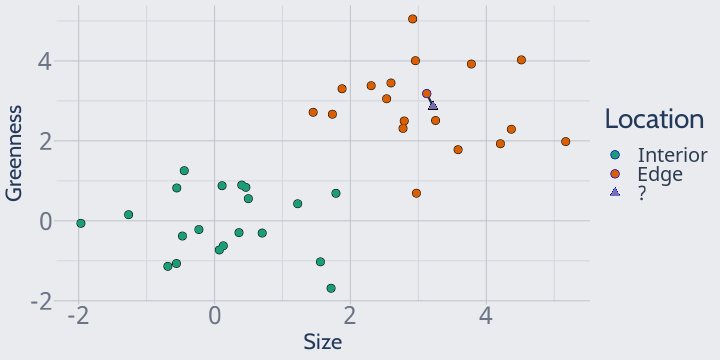
This is exactly how k-nearest neighbors works. For some value of k that you 
choose, KNN looks at the closest k neighbors and predicts whatever the majority
class is.

For instance, if we set k = 1 our model would look at the closest point 
(attached on the graph by
a black line) and predict that our unknown observation was an edge plant:

![](week_10_slides_files/figure-html/unnamed-chunk-3-1.png)

---

We could also imagine, for instance, setting k to 2, in which case KNN would 
look at the two closest plots and still predict edge:

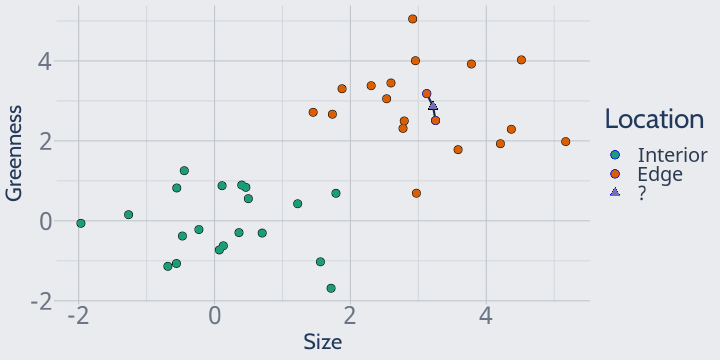
![](week_10_slides_files/figure-html/unnamed-chunk-4-1.png)

---

A k of 2 can sometimes cause problems, however.

For instance, imagine if this plant instead was our mystery point:

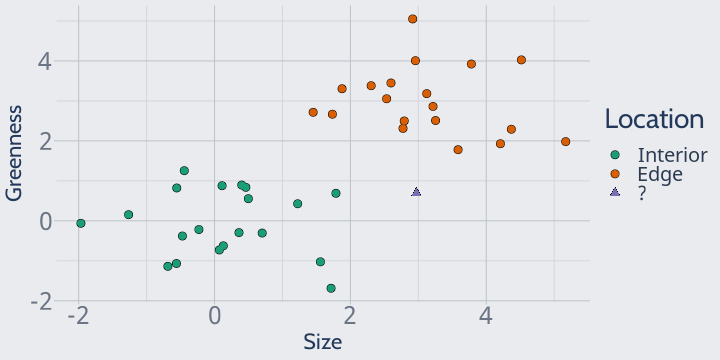
![](week_10_slides_files/figure-html/unnamed-chunk-5-1.png)

---

If we set k to 2 here, we'd have one nearest neighbor from each class:

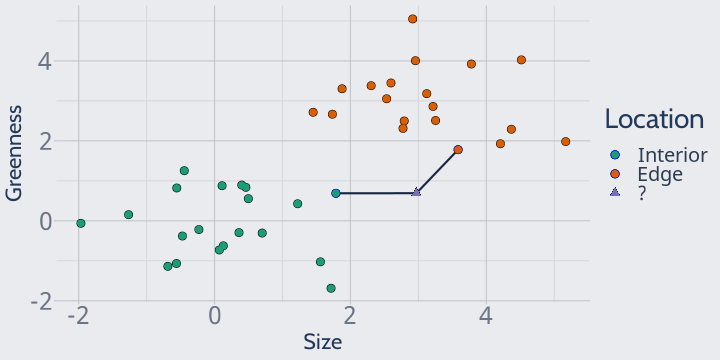
![](week_10_slides_files/figure-html/unnamed-chunk-6-1.png)

In this case, our model would think that both classes are equally likely! What
that means for your predictions depends on the package -- some implementations 
will fail entirely, some will flip a coin, and others will default to one of 
your classes -- but no matter what, it's not an ideal situation.

---

So at least for binary classification, we prefer to always set k to odd values 
so that we don't wind up with ties in our predictions.

For instance, with k = 3 we can easily categorize this plant as an edge plant:

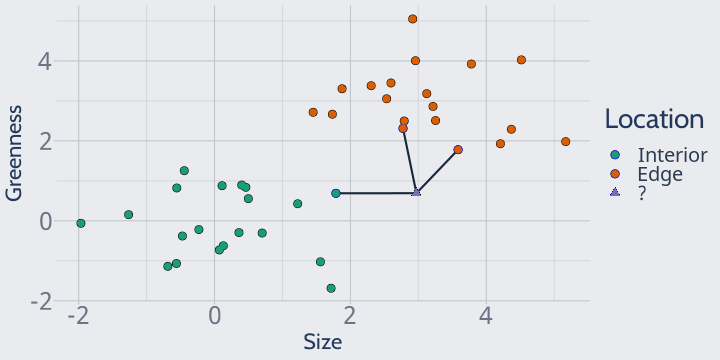
![](week_10_slides_files/figure-html/unnamed-chunk-7-1.png)

---

I know this seems extremely simple, but I think it's useful to think about what
exactly "distance" is representing here -- that is, how we're calculating 
"closeness".

On our 2D graphs, we can see the "closest" point pretty intuitively. We put a 
variable on the X and Y axis, and then the closest point is the one that we can
draw the shortest line between. It's the "nearest" in some combination of both
the X and the Y values.

And we could imagine doing the same thing in 3D: plotting each of our variables
on an axis and then finding the shortest 1D line between two points.

This is effectively what KNN is doing, except in many more dimensions -- as many
dimensions as your data frame has columns. KNN is attempting to find the nearest
neighbors based on all of your variables at once; it's trying to draw that 1D
line in extremely high-dimensional space.

But there's a problem with thinking of closeness in this way. To explain why,
let's go ahead and load our attrition data into R and create our training/test
splits:

```r
library(modeldata)
data(attrition)
set.seed(123)
row_idx <- sample(seq_len(nrow(attrition)), nrow(attrition))
training <- attrition[row_idx < nrow(attrition) * 0.8, ]
testing <- attrition[row_idx >= nrow(attrition) * 0.8, ]
```

---

Our attrition data has many numeric variables. For instance, it has `Age` and
`DailyRate`, both of which were useful predictors back in our decision tree 
models.

Plotted together, they look like this:

```r
library(ggplot2)
training |> 
  ggplot(aes(DailyRate, Age, color = Attrition)) + 
  geom_point() + 
  scale_color_brewer(palette = "Dark2")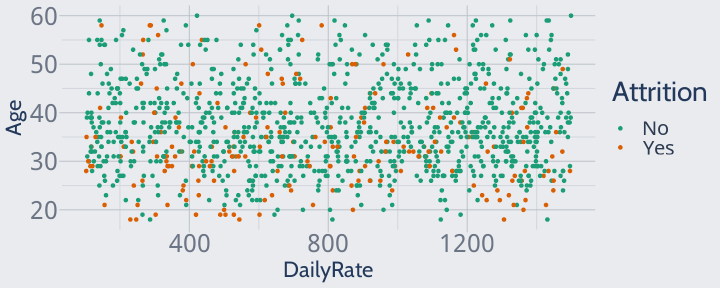
```

![](week_10_slides_files/figure-html/unnamed-chunk-9-1.png)

---

However, this isn't how these variables look to a KNN. KNNs don't understand
the implicit units in our data, or the fact that you can have a lot more 
variation in a daily rate than in age.

To a KNN, a one-unit change in one variable is the same size as a one-unit 
change in another. To a KNN, our scatterplot looks like this:

```r
training |> 
  ggplot(aes(DailyRate, Age, color = Attrition)) + 
  geom_point() + 
  scale_color_brewer(palette = "Dark2") + 
  scale_y_continuous(limits = c(0, max(training$DailyRate))) + 
  scale_x_continuous(limits = c(min(training$Age), max(training$DailyRate)))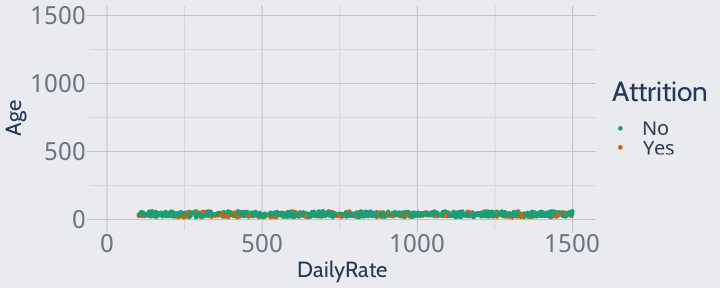
```

![](week_10_slides_files/figure-html/unnamed-chunk-10-1.png)

---

Since all of our data is extremely close in age, the model won't pay any 
attention to age when finding neighbors or making predictions -- which isn't 
great, since we know age is an adequate predictor!

![](week_10_slides_files/figure-html/unnamed-chunk-11-1.png)

---

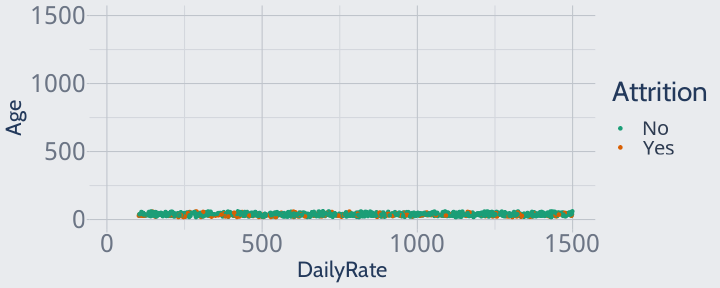
To fix this, we'll have to **rescale** our data so that a one-unit change in
one variable is _actually_ as dramatic as a one-unit change in another.

First, we'll center our data at 0 by subtracting the mean value from each
observation:

```r
library(dplyr)
training |> 
  mutate(across(where(is.numeric), 
                \(x) ((x - mean(x))))) |> 
  ggplot(aes(DailyRate, Age, color = Attrition)) + 
  geom_point() + 
  scale_color_brewer(palette = "Dark2")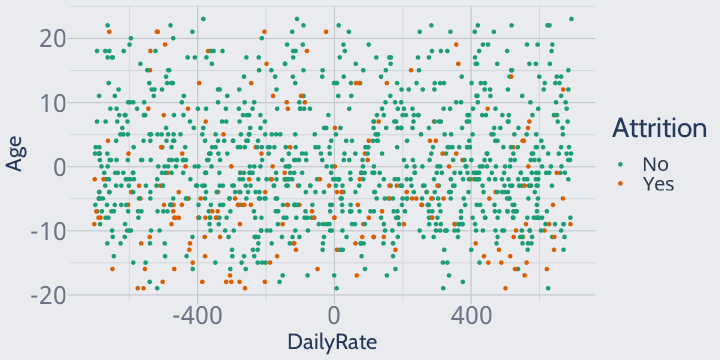
```

![](week_10_slides_files/figure-html/unnamed-chunk-12-1.png)

---

We'll then divide each observation by the original standard deviation of the 
vector.

Our variables are now all rescaled so that one unit represents one standard 
deviation -- an Age value of 1 means that the employee was exactly one standard
deviation above the mean age. This way, a change of 1 means the same thing 
across all of our variables.

```r
training |> 
  mutate(across(where(is.numeric), 
                \(x) ((x - mean(x)) / sd(x)))) |> 
  ggplot(aes(DailyRate, Age, color = Attrition)) + 
  geom_point() + 
  scale_color_brewer(palette = "Dark2")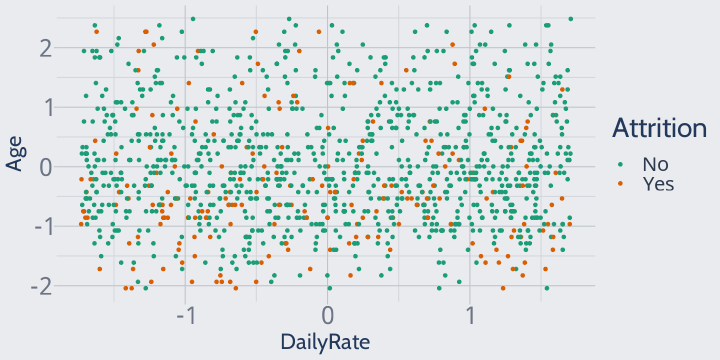
```

![](week_10_slides_files/figure-html/unnamed-chunk-13-1.png)

---

So, because KNN uses all of our variables to calculate distance and doesn't 
understand units in our data, we need to center and scale our variables for the
model to work properly.

The other implication here I want to highlight is that KNNs use _all_ of our
variables to calculate distance between points. Unlike tree-based methods, KNNs
don't select only the most effective variables to use while making predictions.

This means that, unlike tree-based methods, KNNs are susceptible to noisy 
variables, and might benefit from dimension reduction and feature engineering
techniques (like PCA) which we don't cover in this course. This makes KNNs
harder to use and often limits their accuracy compared to other methods.

This is a consistent limitation of kernel-based methods; we'll return to this 
idea next week.

---

So we need to center and scale our variables before fitting a KNN.

However, we don't want to do this directly to our `attrition` data frame, before
we split it into testing and training pieces!

Remember that the testing data is supposed to be entirely unknown to the model 
and the modeler; including testing data in your calculations of mean and 
standard deviation violates that assumption.

This type of mistake, where testing data influences your training data and your
models themselves, is known as **data leakage** and can result in too-optimistic
estimates of model accuracy, as your hold-out set is no longer truly being held
out.

As a result, we need to calculate the mean and standard deviation of each variable
on our training data, and scale both the training and test sets by those values.

While we don't have time to cover much data pre-processing in this course, I 
want to emphasize that this rule applies to anything you do to your data before
fitting a model -- whether it's deciding to filter out variables, rescaling data,
imputation, creating principal components, or anything else, you _need_ to make
sure testing data never influences the data you train your models with.

---

This is where the `recipes` package we mentioned last week really shines. 
You might remember that we can specify our pre-processing steps by creating a
"recipe" object, using `step_` functions to declare what steps we want to 
perform, and then finishing up with `prep()`.

Since we want to center and scale our data, we'll use the `step_center` and
`step_scale` functions in our recipe:

```r
library(recipes)

scaling_recipe <- recipe(Attrition ~ ., data = training) |> 
  step_center(where(is.numeric)) |> 
  step_scale(where(is.numeric)) |> 
  prep()
```

The beauty of `recipes` is that, because we've specified what data to use in
the recipe in our `recipe()` call, our `scaling_recipe` will automatically use
values from our training data to center and scale whatever data we want.

All we have to do is pass our training and testing data to the `bake` function
to rescale our data without any threat of leakage:

```r
training <- bake(scaling_recipe, training)
testing <- bake(scaling_recipe, testing)
```

---

And now we're finally able to get started fitting our first KNN!

The best R package for fitting KNNs is actually one we've used before: `caret`.
We'll load it now:

```r
library(caret)
```

Fitting a KNN is then as simple as using `knn3` just like `lm` or most of the 
other model functions we've seen:

```r
first_knn <- knn3(Attrition ~ ., training)
```

Once that finishes, we'll get a 5-nearest neighbors model object!

```r
first_knn
```

```
## 5-nearest neighbor model
## Training set outcome distribution:
## 
##  No Yes 
## 971 204
```

As usual, we can investigate this model using a confusion matrix (on the next 
slide).

---

```r
confusionMatrix(
  predict(first_knn, testing, type = "class"),
  testing$Attrition,
  positive = "Yes"
)
```

```
## Confusion Matrix and Statistics
## 
##           Reference
## Prediction  No Yes
##        No  258  30
##        Yes   4   3
##                                           
##                Accuracy : 0.8847          
##                  95% CI : (0.8427, 0.9188)
##     No Information Rate : 0.8881          
##     P-Value [Acc > NIR] : 0.6175          
##                                           
##                   Kappa : 0.1154          
##                                           
##  Mcnemar's Test P-Value : 1.807e-05       
##                                           
##             Sensitivity : 0.09091         
##             Specificity : 0.98473         
##          Pos Pred Value : 0.42857         
##          Neg Pred Value : 0.89583         
##              Prevalence : 0.11186         
##          Detection Rate : 0.01017         
##    Detection Prevalence : 0.02373         
##       Balanced Accuracy : 0.53782         
##                                           
##        'Positive' Class : Yes             
## 
```

---

We can also use our old friend the ROC curve to calculate the AUC of this model:

```r
library(pROC)

auc(
  roc(
    testing$Attrition,
    predict(first_knn, testing)[, 2],
    plot = TRUE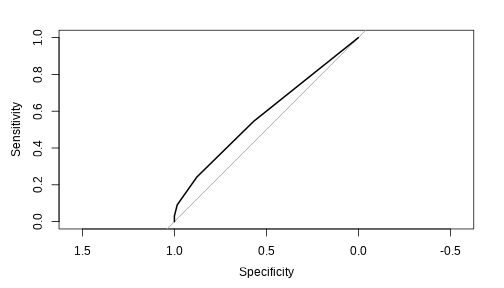
  )
)
```

![](week_10_slides_files/figure-html/unnamed-chunk-20-1.png)

```
## Area under the curve: 0.58
```

It turns out, this model does a pretty bad job predicting our test set.

---

Looking at our specificity rates, it might be helpful if we balance our classes
before predicting.

`knn3` doesn't take weights as an argument, so we'll need
to resample our data in order to balance our training data:

```r
training <- attrition[row_idx < nrow(attrition) * 0.8, ]
testing <- attrition[row_idx >= nrow(attrition) * 0.8, ]

positive_training <- training[training$Attrition == "Yes", ]
negative_training <- training[training$Attrition == "No", ]
n_pos <- nrow(positive_training)

resampled_positives <- sample(1:n_pos, 
                              size = 5 * n_pos, 
                              replace = TRUE)

resampled_positives <- positive_training[resampled_positives, ]
training <- rbind(
  negative_training,
  resampled_positives
)
```

---

We also might get better results from choosing a different value of k. Like
all other hyperparameters, we can tune this via a grid search.

However, cross-entropy is a bad loss function for KNNs. KNNs don't
_really_ predict probability, they just predict whatever class the majority of 
neighbors are.

If we force KNN to report probabilities, what we get back instead are 
percentages of how many neighbors belong to each class. This means that a k of 1
can only predict 100% and 0% probabilities, a k of 3 0%, 33%, 67%, and 100%, and
so on.

Since cross-entropy specifically penalizes confident-but-wrong guesses, this 
means that cross-entropy will usually decrease as k increases and guesses become 
less confident. As a result, cross-entropy will often favor higher values of k
whether or not it improves our actual predictions.

So instead, we'll use our old friend AUC as a loss function to tune KNNs.

---

When we predict with `knn3`, we get a matrix of the "probabilities" 
(really proportions) of each class:

```r
predict(first_knn, testing) |> head(1)
```

```
##             No       Yes
## [1,] 0.7777778 0.2222222
```

To just get our positive probability, we'll index into the data frame:

```r
predict(first_knn, testing)[, 2] |> head(1)
```

```
## [1] 0.2222222
```

And so our function to calculate the AUC looks like this:

```r
calc_auc <- function(model, data) {
  roc(data$Attrition, predict(model, data)[, 2]) |> 
    auc() |> 
    suppressMessages()
}
```

I've also added a `suppressMessages` function here because `roc` is a pretty
chatty function, which can get annoying when running it 100 times.

---

We can then repurpose our `k_fold_cv` function from last time to tune our KNN.
We'll scale our data each iteration to avoid data leakage from the testing fold:

```r
k_fold_cv <- function(data, k, n) {
  per_fold <- floor(nrow(data) / k)
  fold_order <- sample(seq_len(nrow(data)), 
                       size = per_fold * k)
  fold_rows <- split(
    fold_order,
    rep(1:k, each = per_fold)
  )
  vapply(
    fold_rows,
    \(fold_idx) {
      fold_test <- data[fold_idx, ]
      fold_train <- data[-fold_idx, ]
      scaling_recipe <- recipe(Attrition ~ ., data = fold_train) |> 
        step_center(where(is.numeric)) |> 
        step_scale(where(is.numeric)) |> 
        prep()
      
      fold_train <- bake(scaling_recipe, fold_train)
      fold_test <- bake(scaling_recipe, fold_test)
      
      fold_knn <- knn3(Attrition ~ ., fold_train, k = n)
      calc_auc(fold_knn, fold_test)
    },
    numeric(1)
  ) |> 
    mean()
}
```

---

k can go as high as the total number of rows in your data (in which case you'll 
always predict the more common class) or as low as 1 (using only the closest
neighbor), and there's really not a good rule of thumb for what k values to try.

We'll go ahead and try 20 k values evenly spaced between 1 and 401:

```r
tuning_grid <- expand.grid(
  n = floor(seq(1, 401, length.out = 20)),
  auc = NA
)
tuning_grid$n
```

```
##  [1]   1  22  43  64  85 106 127 148 169 190 211 232 253 274 295 316 337 358 379
## [20] 401
```

We still don't want k to be even, however, in order to avoid ties in our 
classifications. We'll add 1 to all our even k values in order to make sure 
we've always got a tiebreaker neighbor:

```r
tuning_grid$n <- ifelse(
  tuning_grid$n %% 2 == 0,
  tuning_grid$n + 1,
  tuning_grid$n
)
tuning_grid$n
```

```
##  [1]   1  23  43  65  85 107 127 149 169 191 211 233 253 275 295 317 337 359 379
## [20] 401
```

---

And with all that done, the code to iterate over our grid is pretty simple:

```r
for (i in seq_len(nrow(tuning_grid))) {
  tuning_grid$auc[i] <- k_fold_cv(
    attrition,
    5,
    n = tuning_grid$n[i]
  )
}

head(arrange(tuning_grid, -auc))
```

```
##     n       auc
## 1  85 0.7572562
## 2 107 0.7544213
## 3 169 0.7537498
## 4 127 0.7526416
## 5 253 0.7514675
## 6  65 0.7509871
```

---

Plotting k makes it pretty obvious that the value of k which maximizes AUC is 
somewhere just under 100.

```r
ggplot(tuning_grid, aes(n, auc)) + 
  geom_line() + 
  geom_point() + 
  labs(x = "k")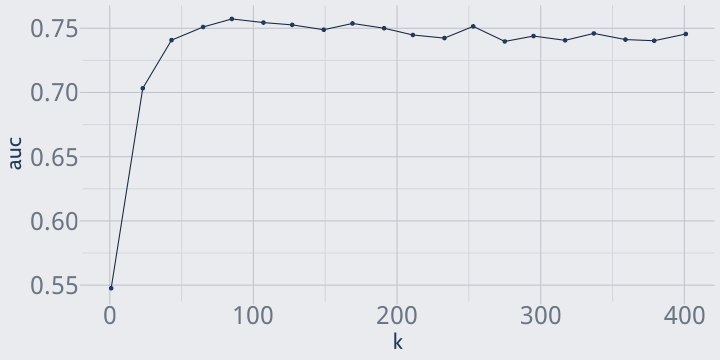
```

![](week_10_slides_files/figure-html/unnamed-chunk-29-1.png)

If we wanted, we could run a second grid search to investigate that area more
thoroughly; right now we'll just run with k = 85.

---

We have to rescale our training and testing sets in order to evaluate our 
hold-out accuracy:

```r
scaling_recipe <- recipe(Attrition ~ ., data = training) |> 
  step_center(where(is.numeric)) |> 
  step_scale(where(is.numeric)) |> 
  prep()

training <- bake(scaling_recipe, training)
testing <- bake(scaling_recipe, testing)
```

And with that done, we can evaluate our accuracy using AUC:

```r
final_knn <- knn3(Attrition ~ ., training, k = 85)
calc_auc(final_knn, testing)
```

```
## Area under the curve: 0.7627
```

As well as via a confusion matrix, on the next page.

---

```r
confusionMatrix(
  predict(final_knn, testing, type = "class"),
  testing$Attrition,
  positive = "Yes"
)
```

```
## Confusion Matrix and Statistics
## 
##           Reference
## Prediction  No Yes
##        No  192  12
##        Yes  70  21
##                                           
##                Accuracy : 0.722           
##                  95% CI : (0.6672, 0.7724)
##     No Information Rate : 0.8881          
##     P-Value [Acc > NIR] : 1               
##                                           
##                   Kappa : 0.2088          
##                                           
##  Mcnemar's Test P-Value : 3.082e-10       
##                                           
##             Sensitivity : 0.63636         
##             Specificity : 0.73282         
##          Pos Pred Value : 0.23077         
##          Neg Pred Value : 0.94118         
##              Prevalence : 0.11186         
##          Detection Rate : 0.07119         
##    Detection Prevalence : 0.30847         
##       Balanced Accuracy : 0.68459         
##                                           
##        'Positive' Class : Yes             
## 
```

---

Overall, this KNN makes pretty adequate predictions! Odds are, we could do 
better with a well-tuned random forest or GBM, but as far as easily-explainable
models go the KNN did alright.

And that's KNN for classification! But the technique can be applied to 
regression tasks as well.

Rather than predict the most common value, KNNs built for regression tasks 
predict the _average_ value of the neighbors (sometimes weighted by distance,
sometimes not, depending on the package you use).

We'll walk through the process quickly, but the fundamental steps are the same
as when using KNNs for classification. First, we'll load our data:

```r
ames <- AmesHousing::make_ames()
row_idx <- sample(seq_len(nrow(ames)), nrow(ames))
training <- ames[row_idx < nrow(ames) * 0.8, ]
testing <- ames[row_idx >= nrow(ames) * 0.8, ]
```

And create our function to calculate RMSE:

```r
calc_rmse <- function(model, data) {
  sqrt(mean((predict(model, data) - data$Sale_Price)^2))
}
```

---

And lastly, we'll repurpose our `k_fold_cv` function. We need to make a few 
changes:

+ Instead of `knn3`, we'll use `knnreg` for regression modeling;

+ We're going to add `-all_outcomes` to our recipe steps, to make sure we don't
  scale and center our sale price;
  
+ And we'll change the formula in `recipe` and `knnreg` to `Sale_Price ~ .` and
  our loss function to `calc_rmse`

The code with these changes is on the next slide.

---

```r
k_fold_cv <- k_fold_cv <- function(data, k, n) {
  per_fold <- floor(nrow(data) / k)
  fold_order <- sample(seq_len(nrow(data)), 
                       size = per_fold * k)
  fold_rows <- split(
    fold_order,
    rep(1:k, each = per_fold)
  )
  vapply(
    fold_rows,
    \(fold_idx) {
      fold_test <- data[fold_idx, ]
      fold_train <- data[-fold_idx, ]
      
      scaling_recipe <- recipe(Sale_Price ~ ., data = fold_train) |> 
        step_center(where(is.numeric), -all_outcomes()) |> 
        step_scale(where(is.numeric),  -all_outcomes()) |> 
        prep()
      
      fold_train <- bake(scaling_recipe, fold_train)
      fold_test <- bake(scaling_recipe, fold_test)
      
      fold_knn <- knnreg(Sale_Price ~ ., fold_train, k = n)
      calc_rmse(fold_knn, fold_test)
    },
    numeric(1)
  ) |> 
    mean()
}
```

---

Just as before, we can iterate through possible k values, find the best one, 
and plot the relationship between k and RMSE:

```r
tuning_grid <- expand.grid(
  n = floor(seq(1, 401, length.out = 20)),
  rmse = NA
)

for (i in seq_len(nrow(tuning_grid))) {
  tuning_grid$rmse[i] <- k_fold_cv(
    training,
    5,
    n = tuning_grid$n[i]
  )
}

head(arrange(tuning_grid, rmse))
```

```
##     n     rmse
## 1  22 34544.91
## 2  43 36479.43
## 3  64 37546.28
## 4  85 38904.05
## 5 106 39746.35
## 6 127 40429.31
```

---

```r
ggplot(tuning_grid, aes(n, rmse)) + 
  geom_line() + 
  geom_point() + 
  labs(x = "k")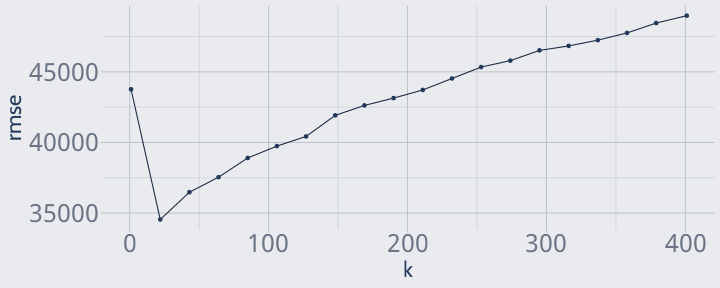
```

![](week_10_slides_files/figure-html/unnamed-chunk-37-1.png)

It looks like the best k is somewhere under 40! We'll run with k = 22 for now.

---

Just as before, we need to rescale our training and testing data before fitting
a KNN to the full training data:

```r
scaling_recipe <- recipe(Sale_Price ~ ., data = training) |> 
  step_center(where(is.numeric), -all_outcomes()) |> 
  step_scale(where(is.numeric), - all_outcomes()) |> 
  prep()

training <- bake(scaling_recipe, training)
testing <- bake(scaling_recipe, testing)
```

And we can now go ahead and evaluate our RMSE:

```r
final_knn <- knnreg(Sale_Price ~ ., training, k = 22)
calc_rmse(final_knn, testing)
```

```
## [1] 29419.37
```

We've done dramatically better with random forests and GBMs, but
KNN at least beats linear regression.

---
class: middle

And that, in a nutshell, is the k-nearest neighbors algorithm.

As I mentioned at the start of these slides, KNN is extremely computationally
inefficient and tends to not create as accurate models as the random forests and
GBMs we've talked about in the past.

However, k-nearest neighbor models are still somewhat prevalent in the 
scientific literature, and are a useful way for us to shift from tree-based 
to kernel-based models.

Next week, we'll wrap up with the most famous kernel-based method of them all,
the support vector machine.

---
class: middle

# References

---

Titles are links:

+ [HOML Chapter 8 (KNNs) and 3 (Feature Engineering)](https://bradleyboehmke.github.io/HOML/knn.html)